FTIR-Spektroskopie zur Bestimmung der optischen Eigenschaften von Halbleitern
Exkurs:
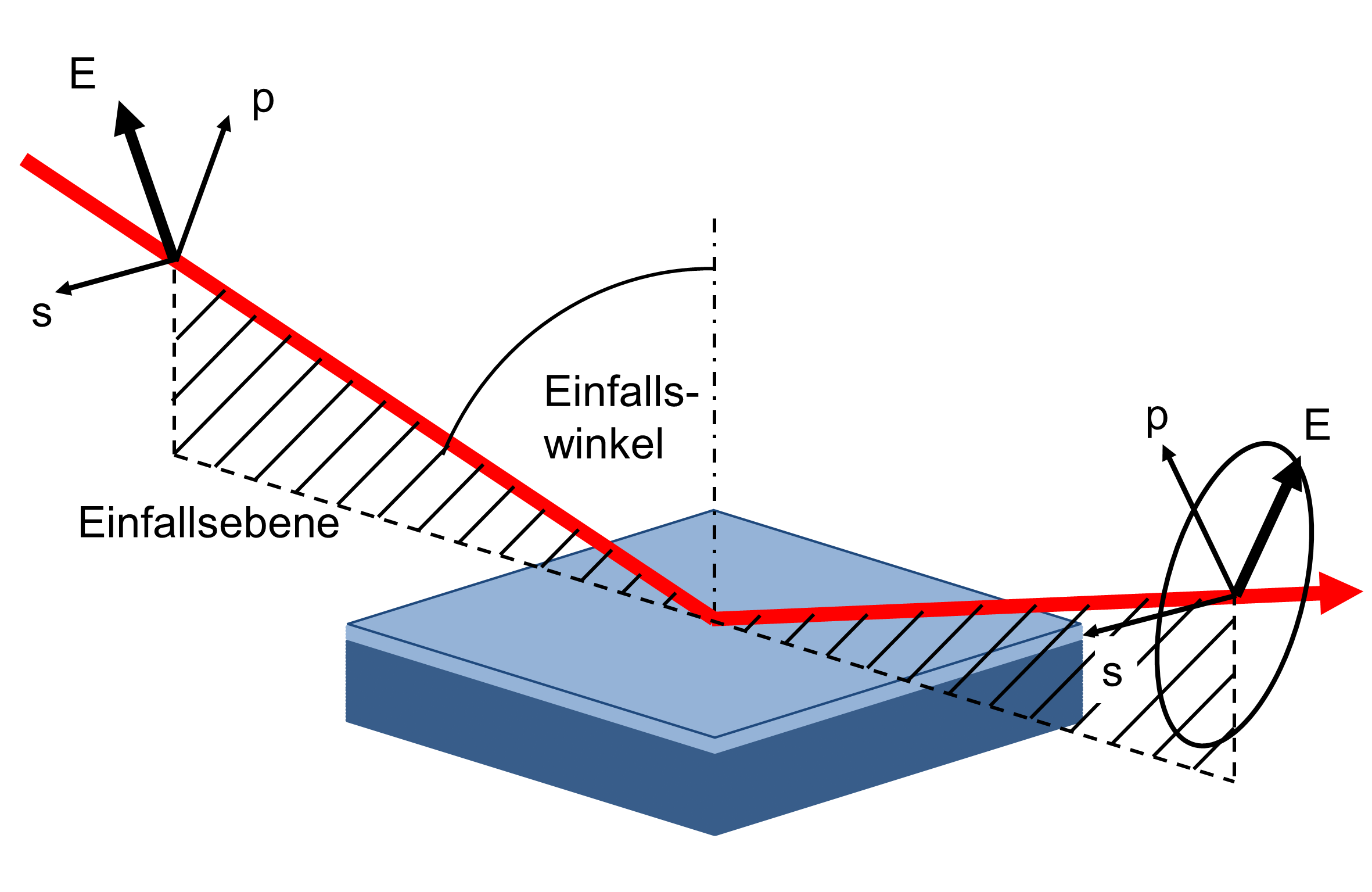
IR-Ellipsometrie
Vortrag:
FTIR & IRSE
FTIR - Spektroskopie
Das Prinzip der FTIR-Spektroskopie (Interferogramm - Spektrum)
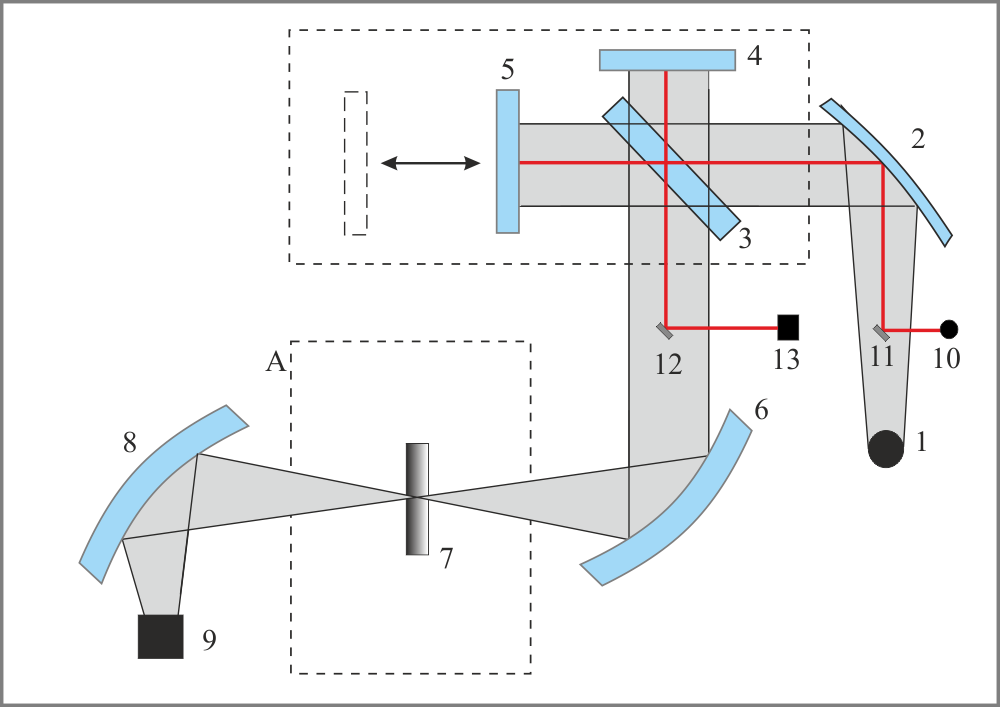
Der wesentliche Unterschied des FTIR-Spektrometers im Vergleich zum Gitterspektrometer ist die Verwendung eines Interferometers. Im Interferometer wird der von der Lichtquelle ausgesandte Strahl in zwei Teilstrahlen zerlegt, die zwei getrennte optische Wege zurücklegen und anschließend wieder interferieren. Danach interagiert der Strahl mit der Probe und gelangt schließlich auf den Detektor. Die optische Wegdifferenz x zwischen den beiden Wegen ist variabel und der Detektor misst die auftreffende Strahlungsintensität I in Abhängigkeit von x. Das Ergebnis I(x) nennt man Interferogramm.
Um zu verdeutlichen, wie das Interferogramm eines Spektrums entsteht, betrachtet man das Spektrum als Summe von monochromatischen Wellen. Das Interferogramm einer monochromatischen Welle ist eine Cosinus-Funktion (siehe Abbildung 1a). Das Interferogramm eines diskreten Spektrums ist die Summe der Interferogramme der enthaltenen monochromatischen Wellen. Abbildung 1b zeigt das Spektrum und Interferogramm für drei monochromatische Wellen. Im kontinuierlichen Fall wird die Summe durch ein Integral ersetzt. Abbildung 1c und 1d zeigen zwei kontinuierliche Spektren und ihre Interferogramme.
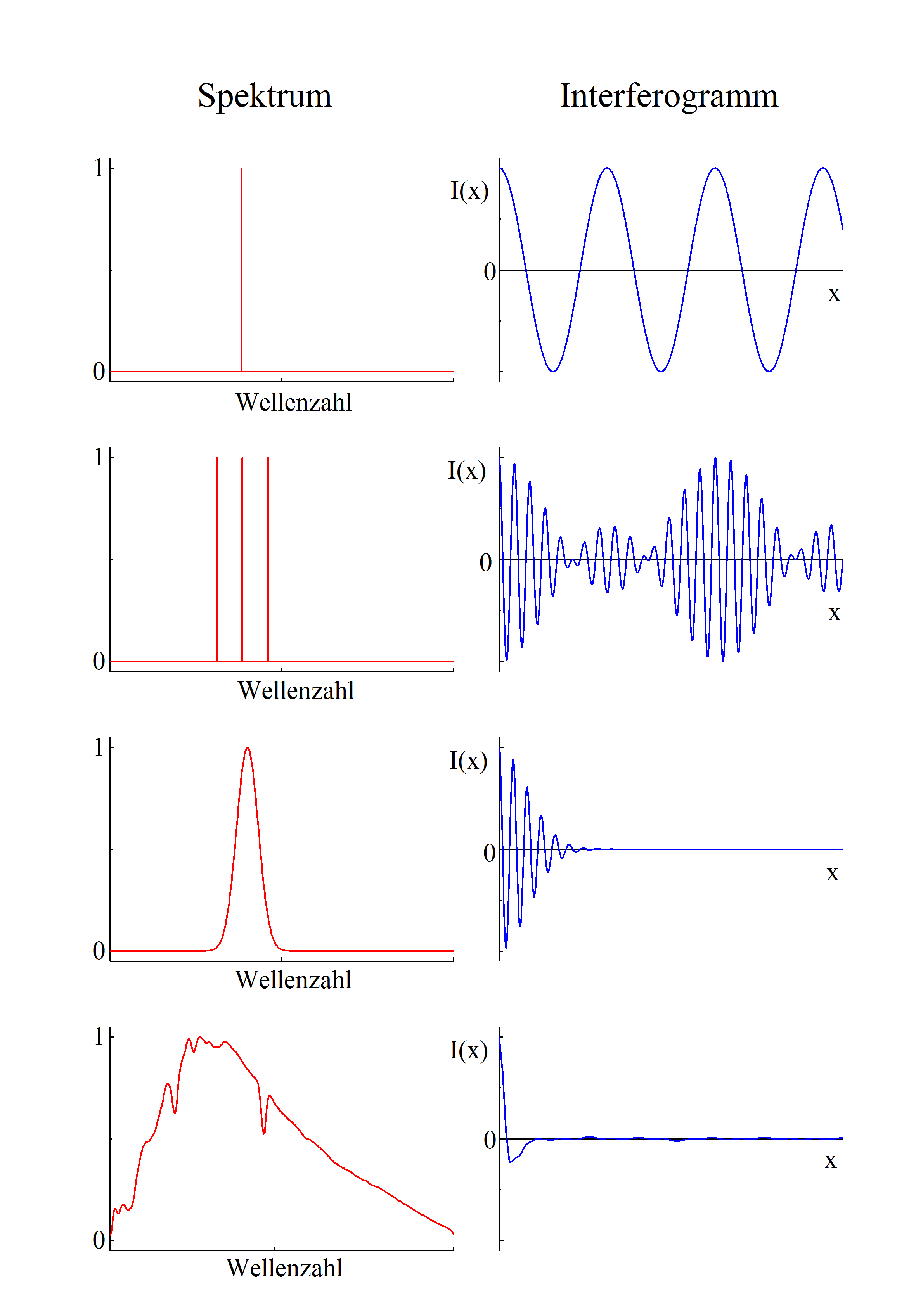
Abbildung 1: Ausgewählte Spektren und ihre Interferogramme
Das Interferogramm ist demnach die Summe oder das Integral über Cosinus-Funktionen. Das erinnert an die Fouriertransformation. Tatsächlich ist das Spektrum die Fouriertransformierte des Interferogramms. Daher leitet sich auch der Name des Messverfahrens Fourier-Transform-Infrarot-Spektroskopie ab.
Praktische Spektrenberechnung
Wie oben beschrieben ist die Spektrenberechnung theoretisch eine Fouriertransformation. Da die Interferogramme aber digitalisiert, begrenzt und nicht symmetrisch bezüglich x=0 gemessen werden, sind zusätzliche Schritte erforderlich. Die praktische Berechnung des Spektrums aus dem gemessenen Interferogramm umfasst die folgenden Schritte:
|
1. Apodisation Das gemessene Interferogramm ist endlich und bricht an seinen Enden abrupt ab. Dadurch kommt es zu einer Störung der Linienform des daraus berechneten Spektrums. Die Apodisation macht aus dem abrupten Abbrechen einen stetigen Abfall, indem das Interferogramm mit einer geeigneten Funktion, zum Beispiel einer Dreiecks oder Trapezfunktion, multipliziert wird. Dadurch wird die Störung der Linienform des berechneten Spektrums unterdrückt. [1,8] 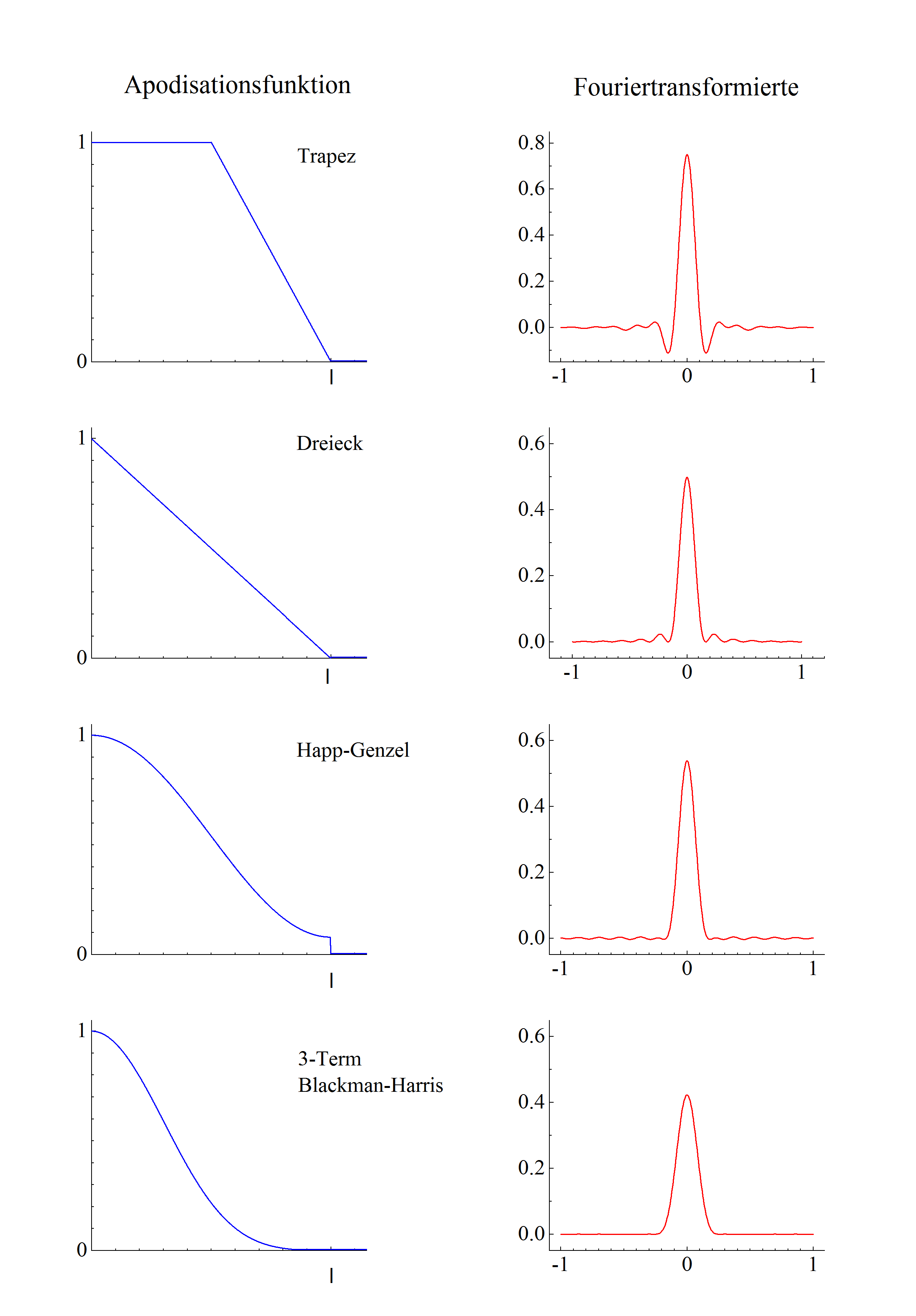 Abbildung 2: Ausgewählte Apodisationsfunktionen und ihre Fouriertransformierten 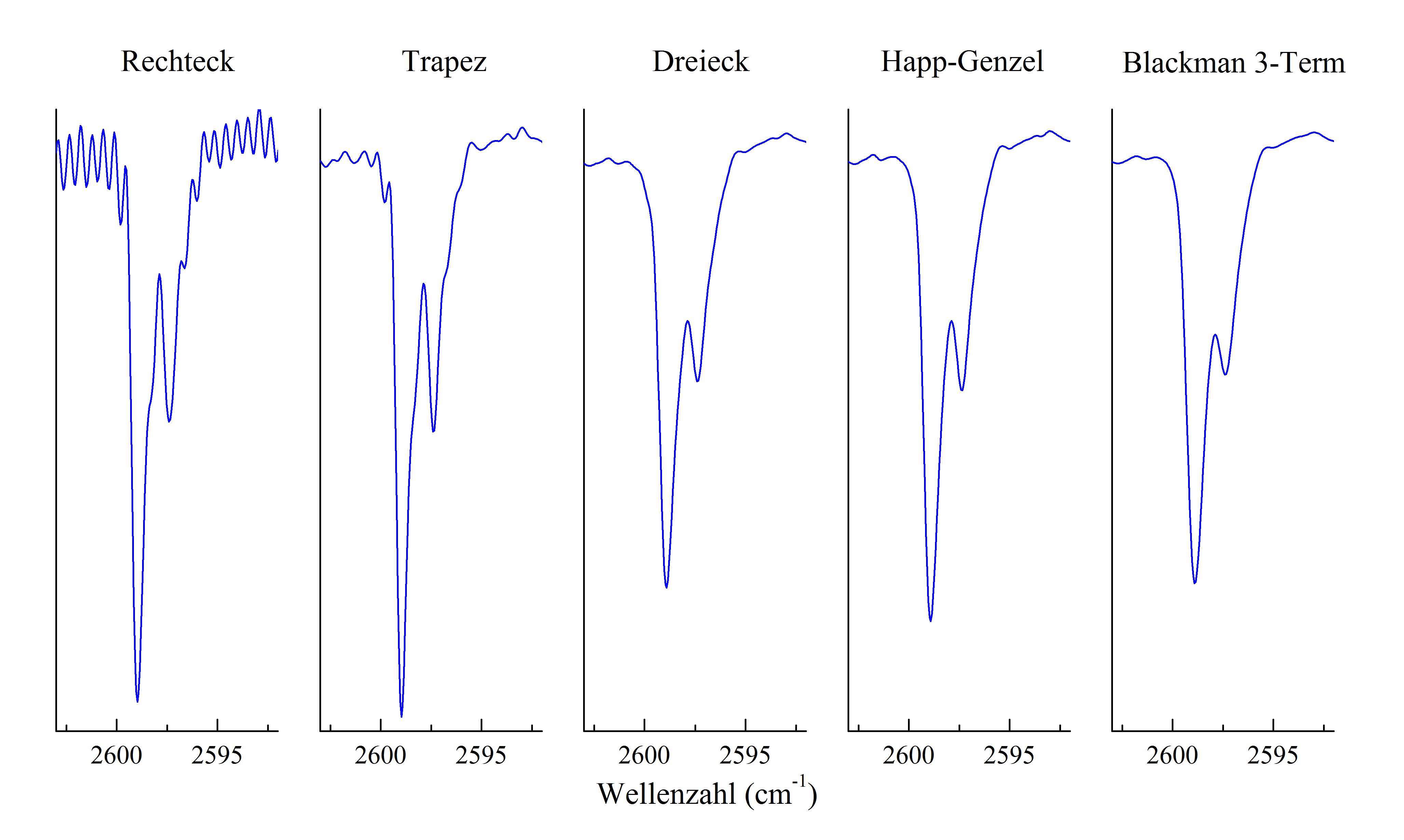 Abbildung 3: Auswirkung der Apodisation auf die Linienform einer Mode des HCl-Spektrums 2. Zerofilling Das Interferogramm wird durch Anhängen von Nullen erweitert, das heißt, die Anzahl der zur Berechnung des Spektrums zu Grunde liegenden Interferogrammpunkte wird erhöht. Dadurch wird die Dichte der berechneten Spektrenpunkte erhöht, was einer Extrapolation entspricht und somit eine Glättung der berechneten Kurve bewirkt. Die Auflösung des Spektrums wird aber nicht erhöht, da die an das gemessene Interferogramm angehängten Nullen keine Informationen enthalten 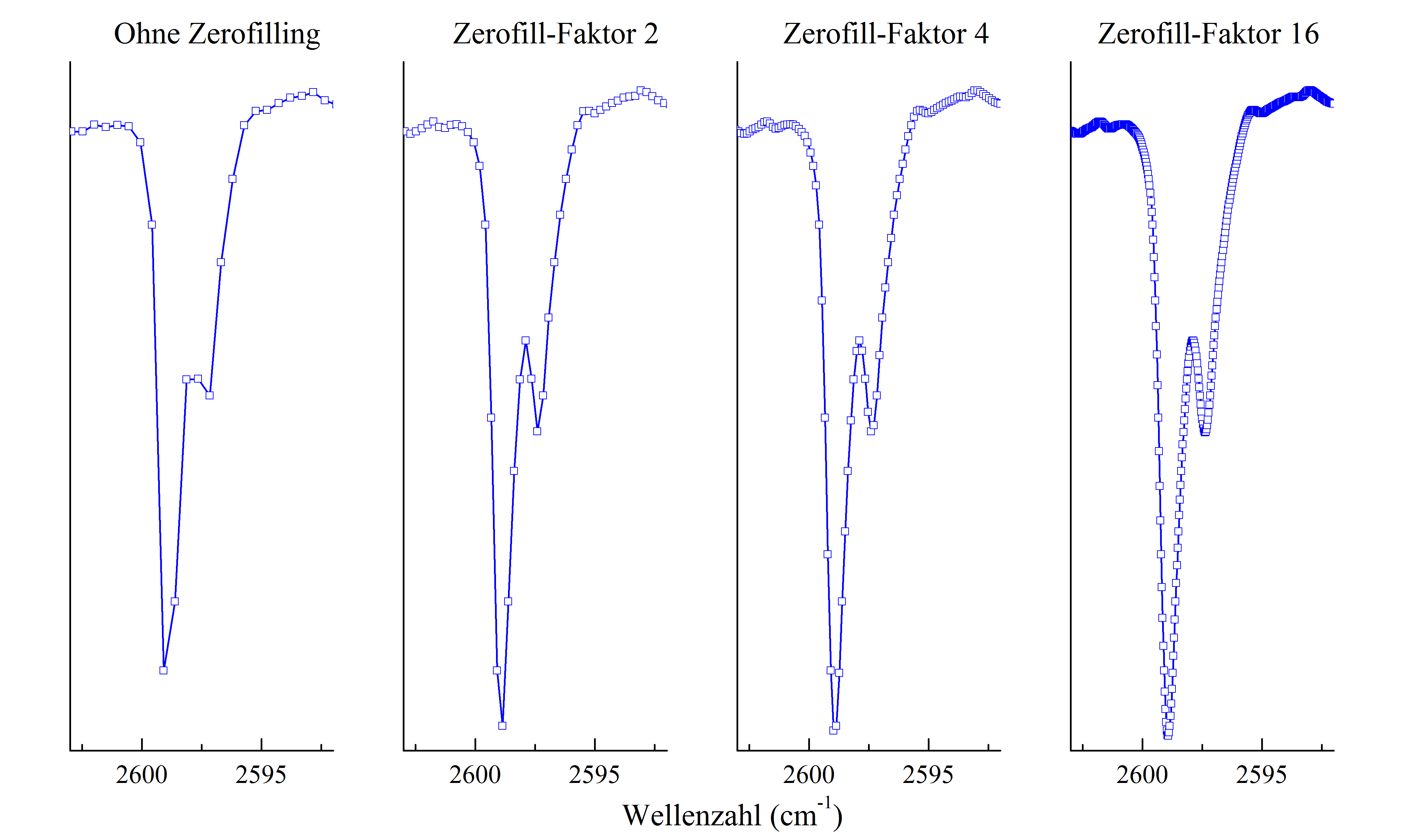 Abbildung 3: Auswirkung des Zerfill-Faktors auf eine Linienform einer Mode des HCl-Spektrums 3. Fouriertransformation Die gemessenen Interferogramme sind digital. Deshalb wird eine digitalisierte Variante der Fouriertransformation benutzt. Aufgrund des hohen Rechenaufwandes verwendet man einen numerischen Algorithmus, der die Anzahl der Rechenschritte deutlich verringert. [1,2] 4. PhasenkorrekturDas gemessene Interferogramm wird meist nur einseitig für x>0 aufgenommen. Dadurch ist das Ergebnis der Fouriertransformation ein komplexes Spektrum. Die Phasenkorrektur berechnet aus dem komplexen das gesuchte reelle Spektrum. 5. Division durch ein ReferenzspektrumAls letzter Schritt wird das Spektrum durch ein Referenzspektrum, das ohne Probe gemessen wurde, dividiert und man erhält das Probenspektrum. |
Vor- und Nachteile
Die FTIR-Spektroskopie hat im Vergleich zu Gittersprektrometern einige wesentliche Vorteile. Aufgrund der umfangreichen Mathematik kann es aber auch zu Problemen kommen.
VorteileJaquinot (Lichtleitwert-, Throughput-)-VorteilIm FTIR-Spektrometer wird die Probe mit einem kreisförmig ausgedehnten Lichtbündel bestrahlt. Im Gegensatz dazu arbeiten Gitterspektrometer mit einem Lichtspalt. Ergebnis ist ein höherer Lichtleistungsdurchgang des FTIR-Spektrometers. Multiplex (Fellget-)-VorteilMan verwendet bei der FTIR-Spektroskopie immer das gesamte Spektrum einer infraroten Strahlungsquelle, das heißt, die Probe wird kontinuierlich mit allen Wellenlängen bestrahlt. Schwankungen im Spektrum der Lichtquelle beeinflussen somit alle und nicht nur ausgewählte Bereiche des berechneten Spektrums und verhindern somit mögliche Verzerrungen. Connes-Vorteil (Wellenzahlgenauigkeit)Die Position des beweglichen Spiegels wird mit Hilfe der Wellenlänge eines Lasers bestimmt, die genau bekannt und konstant ist. Dadurch ergibt sich eine hohe Genauigkeit beim Messen der optischen Wegdifferenz x, die bei der Berechnung des Spektrums eine hohe Wellenzahlgenauigkeit nach sich zieht. MesszeitDie Messzeit für ein einzelnes Interferogramm ist so gering, dass man mit einem FTIR-Spektrometer zeitlich veränderliche Prozesse, zum Beispiel chemische Reaktionen, verfolgen kann. AuflösungDie Auflösung der Gitterspektrometer wird durch die Verringerung eines Spalts, den der Lichtstrahl passiert, realisiert. Ein kleinerer Spalt reduziert die Strahlungsintensität. Das maximale Auflösungsvermögen von Gitterspektrometern ist demnach begrenzt. Mit FTIR-Spektrometern kann man höhere Auflösungsvermögen erreichen, indem man die Länge des gemessenen Interferogramms erhöht. Ergebnis ist eine höhere mögliche Auflösung der FTIR-Spektrometern im Vergleich zu Gitterspektrometern. NachteileDigitalisierung (Picket-Fence-Effekt)Das gemessene Interferogramm und das daraus berechnete Spektrum sind digitalisiert. Fallen die berechneten Spektrenpunkte nicht mit einer vorhandenen Linie des Spektrums zusammen, wird die Linie verkleinert dargestellt oder sogar weggeschnitten. Diesen Effekt nennt man 'Picket-Fence-Effekt'. Er kann durch 'Zerofilling' beseitigt werden. Endliche Interferogrammlänge (Leakage-Effekt)Aufgrund der endlichen Interferogrammlänge ist die Linienform des berechneten Spektrums gestört. Diesen Effekt nennt man 'Leakage-Effekt'. Er kann mit Hilfe der 'Apodisation' verringert werden. AliasingDer Messbereich wird durch eine Faltungswellenzahl nach oben begrenzt. Treten im gemessenen Spektrum Intensitäten oberhalb dieser Wellenzahl auf, werden diese auf den Bereich unterhalb zurückgespiegelt und überlagern das zu messende Spektrum. Dieser Effekt kann durch Einsatz von Filtern, die nur für Licht des gewünschten Wellenzahlbereichs duchlässig sind, ausgeschlossen werden. RechenaufwandDie Auswertung der gemessenen Daten erfordert im Gegensatz zu Gitterspektrometern einen hohen Rechenaufwand. Durch den Einsatz von Computern ist dieser Punkt heute aber praktisch uninteressant. |
Literatur
| [1] | T. Butz: Fouriertransformation für Fußgänger; Verlag B. G. Teubner, Leipzig, 1998. |
| [2] | J. W. Cooley and J. W. Tukey; Math. Comput. 19 (1965)297. |
| [3] | P. S. Griffiths and J. A. de Haseth: Fourier Transform Infrared Spectroscopy; John Wiley & Sons, New York, 1986. |
| [4] | J. Gronholz und W. Herres: Understanding FT-IR Data Processing; I & C Reprint 1(84)& 3(85). http://www.ccmr.cornell.edu/wp-content/uploads/sites/2/2015/11/Understanding_FTIR.pdf |
| [5] | H. Günzler: Infrarot-Spektroskopie; Springer, Berlin, 1996. |
| [6] | H. Günzler und H. Böck: IR-Spektroskopie, Eine Einführung; Verlag Chemie, Weinheim, 1990. |
| [7] | D. Haarer und H. W. Spiess: Spektroskopie amorpher und kristalliner Festkörper; Steinkopff-Verlag, Darmstadt, 1995. |
| [8] | F. J. Harris: On the use of windows for harmonic analysis with discrete fourier transform; Proceedings of the IEEE, 66 (1978) 51. |
| [9] | J. M. Hollas: Modern Spektroscopy; John Wiley & Sons, New York, 1992. |
| [10] | H. Kuzmany: Festkörperspektroskopie; Springer, Berlin, 1990. |
WWW-Links
| [1] | www.ir-spektroskopie.de |
| [2] | FTIR-Spektrometer (Wikipedia) |



| Carsten Bundesmann, 2001 & 2014 | [Zurück zum Seitenanfang] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||